Assumptions

Last Updated: 03, December, 2024 at 09:21

Read some data
Assumption 1: Linearity of model
Assumption 2: Normal distribution of the errors
Assumption 3: Homoscedasticity
More examples
- Heteroscedasticity: Gambling data
- Non-linear relationship: Pima data

Read some data

library(tidyverse)

## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.2 ──
## ✔ ggplot2 3.4.0      ✔ purrr   1.0.2 
## ✔ tibble  3.1.8      ✔ dplyr   1.0.10
## ✔ tidyr   1.2.1      ✔ stringr 1.4.1 
## ✔ readr   2.1.3      ✔ forcats 0.5.2 
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag()    masks stats::lag()

body_data <-read_csv('data/body.csv')

## Rows: 507 Columns: 25
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## dbl (25): Biacromial, Biiliac, Bitrochanteric, ChestDepth, ChestDia, ElbowDi...
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

vik_data <-read_csv('data/vik_table_9_2.csv')

## Rows: 12 Columns: 4
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## dbl (4): Person, Y, X1, X2
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

Assumption 1: Linearity of model

Example 1

plot(vik_data$X1, vik_data$Y)

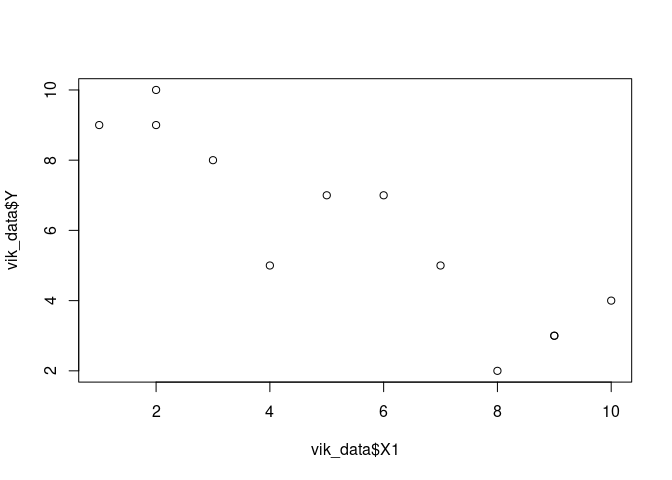
model <- lm(Y ~ X1, data = vik_data)
plot(fitted(model), resid(model))

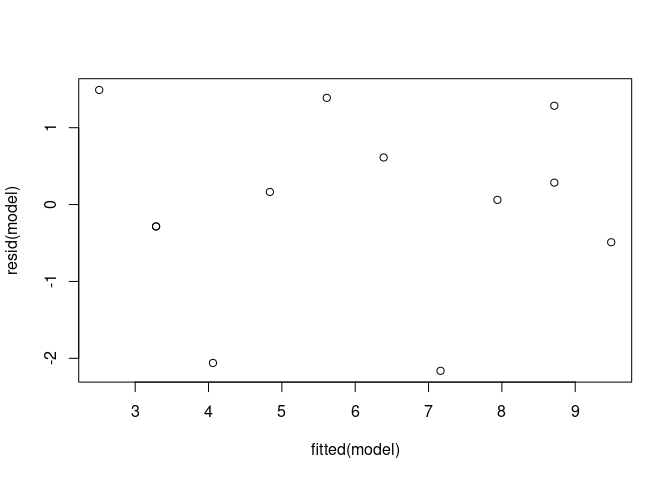Let’s create the diagnostic plots. For our purposes, we will only look at the top two plots.

# Split the plotting panel into a 2 x 2 grid. Such that we get the four plots
# in 4 separate panels.
par(mfrow = c(2, 2))
plot(model)

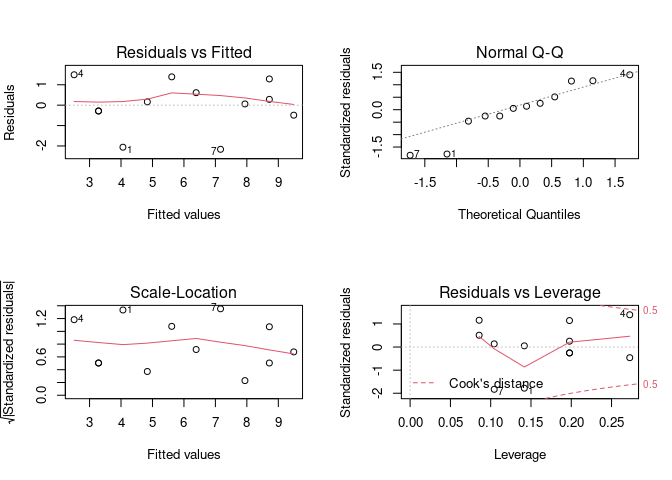
# We can reset the plotting panel using this code: par(mfrow = c(1, 1))

Example 2

x_data <- runif(100)
y_data <- x_data^3 + rnorm(100, sd=0.05)
fake <- tibble(x_data=x_data, y_data = y_data)
model <- lm(y_data ~ x_data, data = fake)
par(mfrow = c(1, 1)) 
plot(x_data, y_data)
abline(model, col='red')

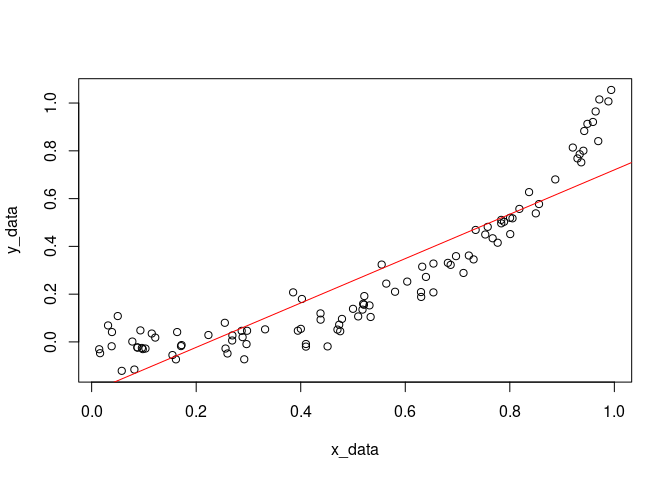
model <- lm(y_data ~ x_data, data = fake)
summary(model)

## 
## Call:
## lm(formula = y_data ~ x_data, data = fake)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.22963 -0.10576 -0.01829  0.09487  0.34005 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -0.20838    0.02650  -7.862 4.99e-12 ***
## x_data       0.92877    0.04503  20.626  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.1346 on 98 degrees of freedom
## Multiple R-squared:  0.8128, Adjusted R-squared:  0.8109 
## F-statistic: 425.4 on 1 and 98 DF,  p-value: < 2.2e-16

par(mfrow = c(2, 2))  # Split the plotting panel into a 2 x 2 grid
plot(model)

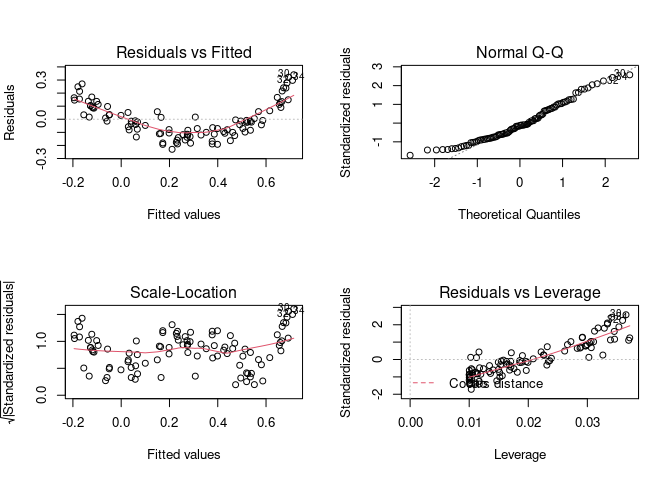
par(mfrow = c(1, 1)) 

Let’s run the model on transformed data and look at the diagnostic plots again.

model <- lm(y_data ~ I(x_data^3), data = fake)
par(mfrow = c(2, 2))  # Split the plotting panel into a 2 x 2 grid
plot(model)

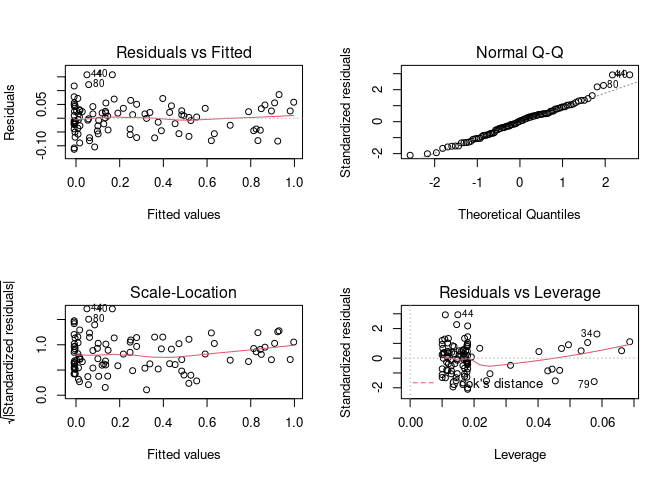
par(mfrow = c(1, 1)) 

Example 3

This demonstrates that the diagnostic plots can also be used when we have multiple predictors (in this case plotting the dependent vs the independents might be difficult or impossible).

x1_data <- runif(100)
x2_data <- runif(100)
y_data <- x1_data^3 + x2_data^3
fake <- tibble(x1_data=x1_data,x2_data=x2_data, y_data = y_data)
model <- lm(y_data ~ x1_data + x2_data, data = fake)
par(mfrow = c(2, 2))  # Split the plotting panel into a 2 x 2 grid
plot(model)

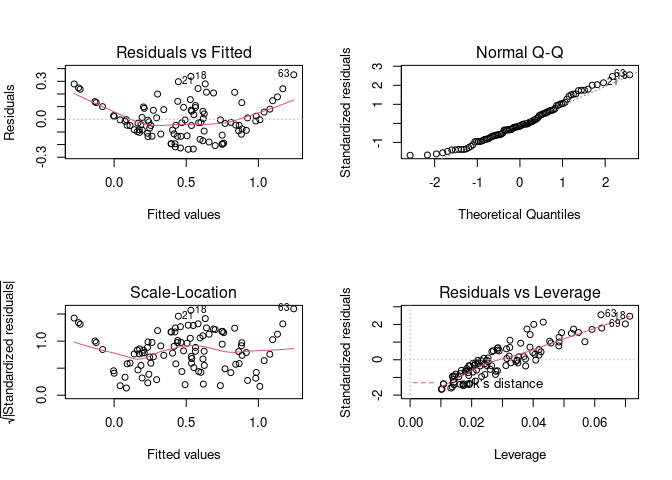
par(mfrow = c(1, 1))

Example 4

Finally, an example with real data.

model <- lm(Weight ~ Height, data = body_data)
par(mfrow = c(2, 2))  # Split the plotting panel into a 2 x 2 grid
plot(model)

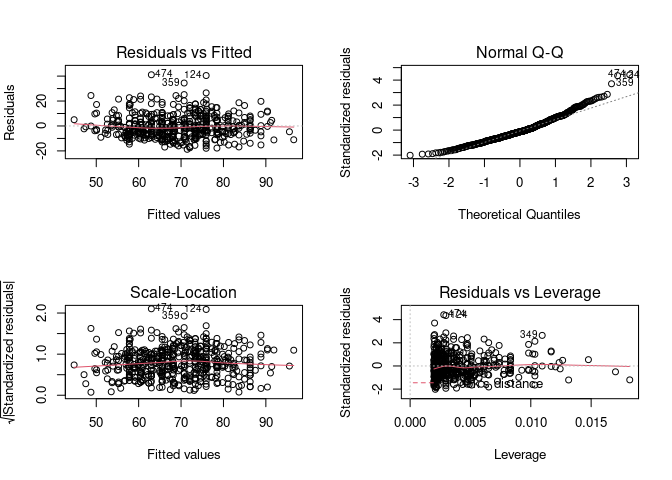
par(mfrow = c(1, 1)) 

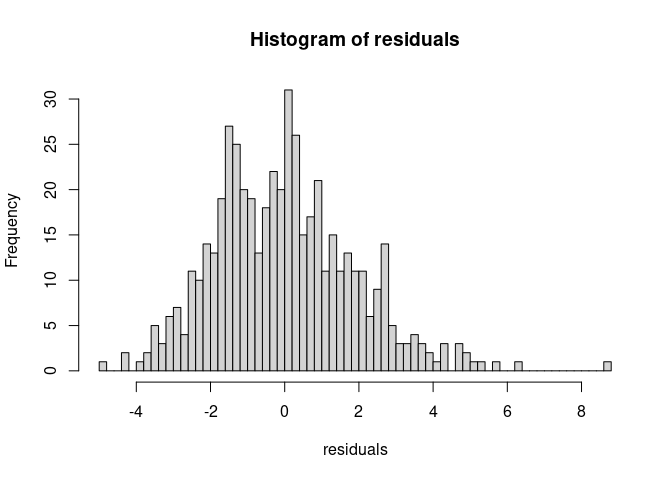
Assumption 2: Normal distribution of the errors

model <- lm(Bicep ~ Shoulder, data = body_data)
residuals <- resid(model)
hist(residuals, 50)

par(mfrow = c(2, 2))  # Split the plotting panel into a 2 x 2 grid
plot(model)

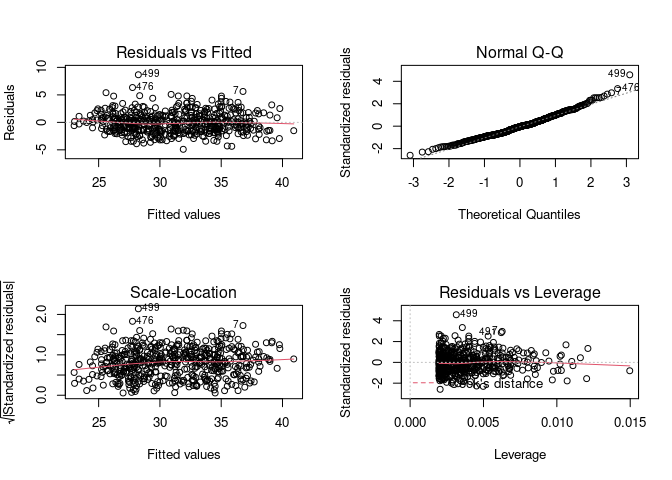
par(mfrow = c(1, 1)) 

Assumption 3: Homoscedasticity

I created a data set with heteroscedasticity. The gambling data below might be a good example as well.

n<-500
errors <-rnorm(n, sd=seq(0.1,5, length.out=n))
x<-runif(n)
x<-sort(x)
y<- (20 * x) + errors
plot(x, y)

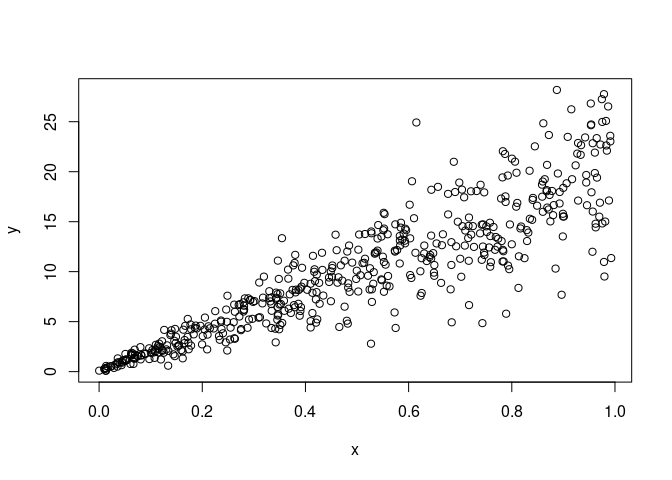
fake<-tibble(x=x, y=y)
model <- lm(y~x, data = fake) 

The model is still fitted properly!

summary(model)

## 
## Call:
## lm(formula = y ~ x, data = fake)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -10.2339  -1.3420   0.0339   1.2422  12.6182 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.03805    0.25641   0.148    0.882    
## x           19.94614    0.44861  44.463   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.891 on 498 degrees of freedom
## Multiple R-squared:  0.7988, Adjusted R-squared:  0.7984 
## F-statistic:  1977 on 1 and 498 DF,  p-value: < 2.2e-16

plot(x, y)
abline(model, col='red')

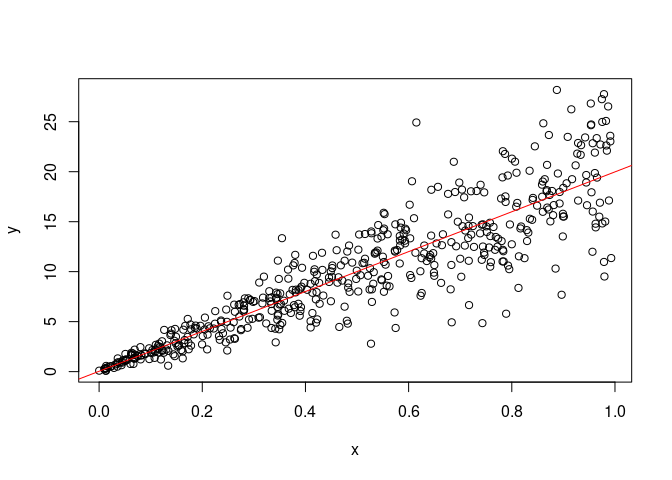
par(mfrow = c(2, 2))  # Split the plotting panel into a 2 x 2 grid
plot(model)

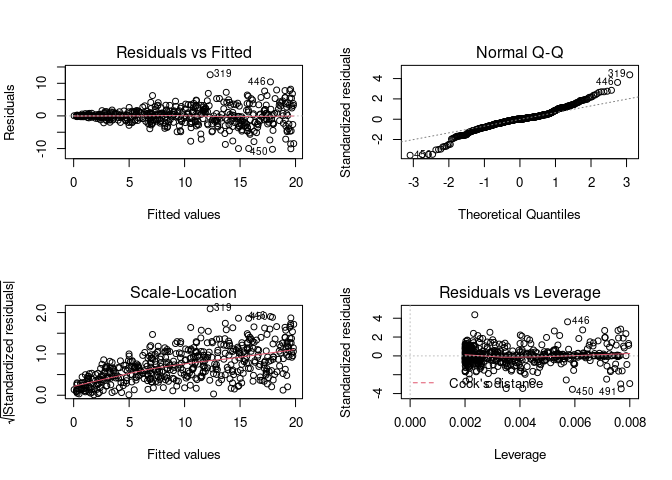
par(mfrow = c(1, 1)) 

More examples

Heteroscedasticity: Gambling data

The teengamb data frame has 47 rows and 5 columns. A survey was conducted to study teenage gambling in Britain. This data frame contains the following columns:

sex 0=male, 1=female
Socioeconomic status score based on parents’ occupation
Income in pounds per week
Verbal score in words out of 12 correctly deﬁned
Gamble expenditure on gambling in pounds per year

library(faraway)
data <- teengamb
head(data)

##   sex status income verbal gamble
## 1   1     51   2.00      8    0.0
## 2   1     28   2.50      8    0.0
## 3   1     37   2.00      6    0.0
## 4   1     28   7.00      4    7.3
## 5   1     65   2.00      8   19.6
## 6   1     61   3.47      6    0.1

model<- lm(gamble~income, data=data)

plot(data$income, data$gamble)

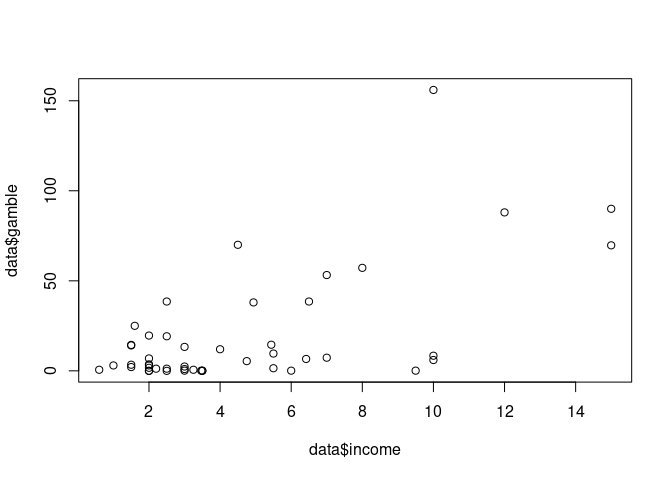
summary(model)

## 
## Call:
## lm(formula = gamble ~ income, data = data)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -46.020 -11.874  -3.757  11.934 107.120 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   -6.325      6.030  -1.049      0.3    
## income         5.520      1.036   5.330 3.05e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 24.95 on 45 degrees of freedom
## Multiple R-squared:  0.387,  Adjusted R-squared:  0.3734 
## F-statistic: 28.41 on 1 and 45 DF,  p-value: 3.045e-06

par(mfrow = c(2, 2))  # Split the plotting panel into a 2 x 2 grid
plot(model)

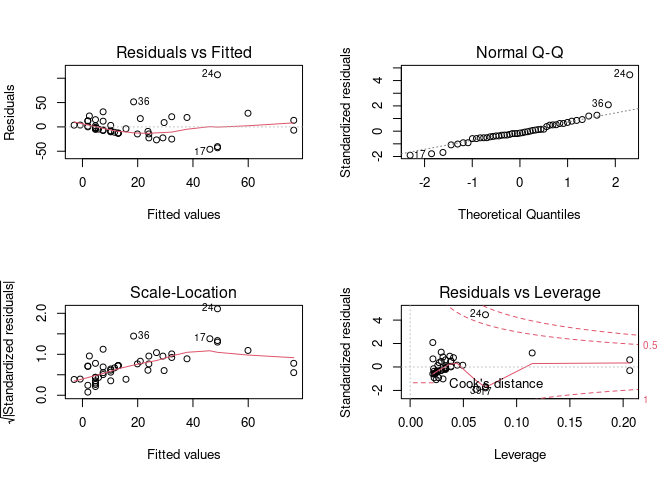
par(mfrow = c(1, 1)) 

plot(data$status,data$gamble)

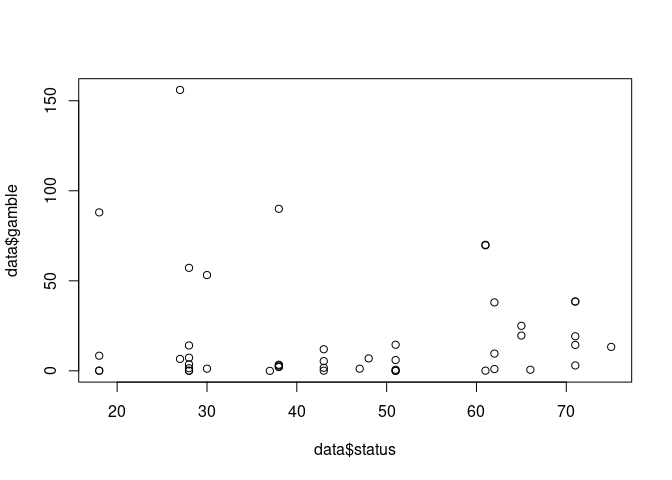
Non-linear relationship: Pima data

The National Institute of Diabetes and Digestive and Kidney Diseases conducted a study on 768 adult female Pima Indians living near Phoenix. The dataset contains the following variables

Number of times pregnant
Plasma glucose concentration at 2 hours in an oral glucose tolerance test
Diastolic blood pressure (mm Hg)
Triceps skin fold thickness (mm) insulin 2-Hour serum insulin (mu U/ml)
Body mass index (weight in kg/(height in metres squared))
Diabetes pedigree function age Age (years)
Test whether the patient shows signs of diabetes (coded 0 if negative, 1 if positive)

data<-pima
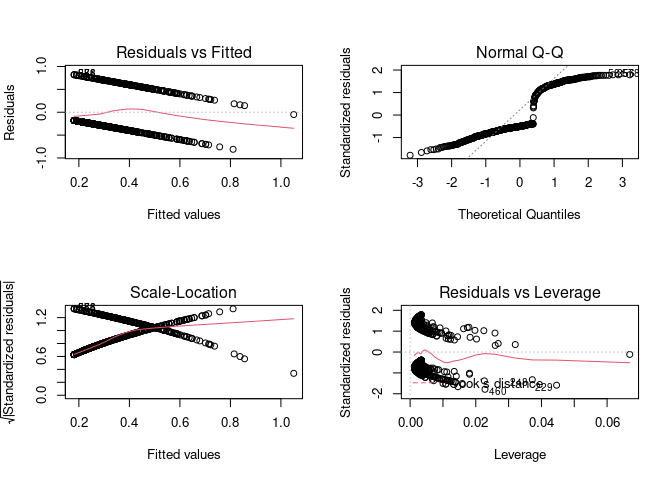
model <-lm(test ~ age + insulin, data=data)

par(mfrow = c(2, 2))  # Split the plotting panel into a 2 x 2 grid
plot(model)

par(mfrow = c(1, 1)) 