The LM with categorical and continuous predictors predictors (ANCOVA)
Last Updated: 02, November, 2023 at 09:21
library(tidyverse)
## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.2 ──
## ✔ ggplot2 3.4.0 ✔ purrr 0.3.5
## ✔ tibble 3.1.8 ✔ dplyr 1.0.10
## ✔ tidyr 1.2.1 ✔ stringr 1.4.1
## ✔ readr 2.1.3 ✔ forcats 0.5.2
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag() masks stats::lag()
library(readxl)
data <- read_excel('data/vik_table_17_2.xlsx')
One-way anova
model1 <- lm(weight ~ sex, data = data)
summary(model1)
##
## Call:
## lm(formula = weight ~ sex, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -11.00 -6.25 1.00 6.25 10.00
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 12.000 2.114 5.676 1.04e-05 ***
## sexM 2.000 2.990 0.669 0.511
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 7.324 on 22 degrees of freedom
## Multiple R-squared: 0.01993, Adjusted R-squared: -0.02461
## F-statistic: 0.4475 on 1 and 22 DF, p-value: 0.5105
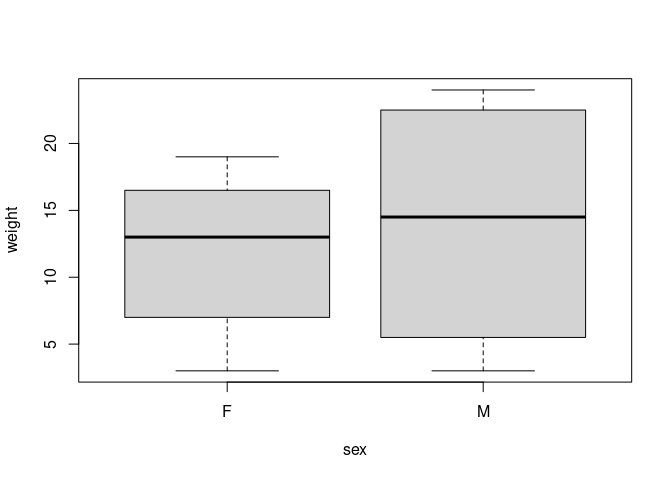
boxplot(weight ~ sex, data = data)
Ancova
model2 <- lm(weight ~ sex * age, data = data)
summary(model2)
##
## Call:
## lm(formula = weight ~ sex * age, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -7.959 -3.085 -1.038 1.540 8.041
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 43.7449 15.9580 2.741 0.0126 *
## sexM 44.0326 20.2885 2.170 0.0422 *
## age -1.5612 0.7822 -1.996 0.0598 .
## sexM:age -1.9243 0.9791 -1.965 0.0634 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.471 on 20 degrees of freedom
## Multiple R-squared: 0.668, Adjusted R-squared: 0.6181
## F-statistic: 13.41 on 3 and 20 DF, p-value: 5.036e-05
model.matrix(model2)
## (Intercept) sexM age sexM:age
## 1 1 0 21 0
## 2 1 0 22 0
## 3 1 0 22 0
## 4 1 0 22 0
## 5 1 0 21 0
## 6 1 0 19 0
## 7 1 0 20 0
## 8 1 0 19 0
## 9 1 0 18 0
## 10 1 0 17 0
## 11 1 0 21 0
## 12 1 0 22 0
## 13 1 1 23 23
## 14 1 1 24 24
## 15 1 1 25 25
## 16 1 1 23 23
## 17 1 1 22 22
## 18 1 1 21 21
## 19 1 1 18 18
## 20 1 1 18 18
## 21 1 1 19 19
## 22 1 1 20 20
## 23 1 1 20 20
## 24 1 1 21 21
## attr(,"assign")
## [1] 0 1 2 3
## attr(,"contrasts")
## attr(,"contrasts")$sex
## [1] "contr.treatment"
females <- filter(data, sex == 'F')
males <- filter(data, sex == 'M')
coefs <- coefficients(model2)
prediction_females <- coefs[1] + coefs[3] * females$age
prediction_males <- coefs[1] + coefs[2] +coefs[3] * males$age + coefs[4] * males$age
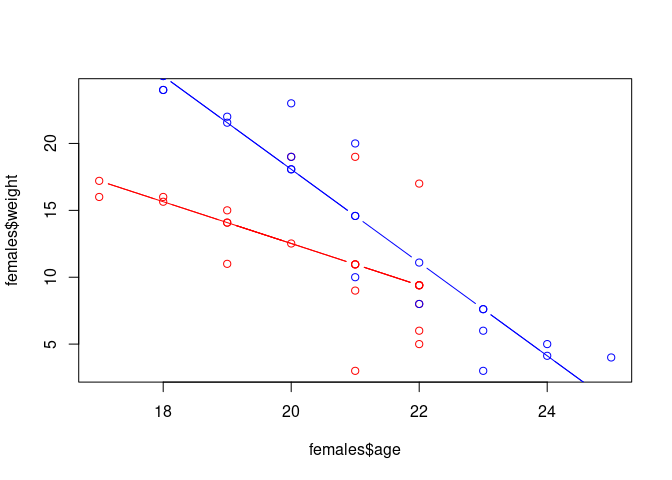
plot(females$age, females$weight, col='red', xlim = range(data$age), ylim = range(data$weight))
points(females$age, prediction_females, type='b', col='red')
points(males$age, males$weight, col='blue')
points(males$age, prediction_males, type='b', col='blue')
# To double check my equations
# points(data$age, model2$fitted.values, col='green')
# my_predications <- c(prediction_females, prediction_males)
# r_predications <- unname(model2$fitted.values)
Compare models
anova(model1, model2)
## Analysis of Variance Table
##
## Model 1: weight ~ sex
## Model 2: weight ~ sex * age
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 22 1180.00
## 2 20 399.78 2 780.22 19.516 1.993e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1