Simple Regression

Last Updated: 19, November, 2024 at 09:23

• Before we start…
• Functions we will use
• First example: body data
  • Read Data
  • Run simple regression model
  • Compare with correlation
  • Get the predicted values
    • For the existing independent variable values
    • For new independent variable values
  • Second example: Vik data
  • Easier regression line
  • Confidence intervals
    • Confidence intervals for the predictions
    • Confidence intervals for the coefficients

Before we start…

Download the following data sets:

• vik_table_9_2.csv
• body.csv

Functions we will use

• lm, to fit a linear model
• summary, to get the results from a linear model
• anova, to get more results from a linear model (or to compare models)
• predict, to predict new values
• abline, to plot a regression line

First example: body data

Read Data

library(tidyverse)

## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.2 ──
## ✔ ggplot2 3.4.0      ✔ purrr   1.0.2 
## ✔ tibble  3.1.8      ✔ dplyr   1.0.10
## ✔ tidyr   1.2.1      ✔ stringr 1.4.1 
## ✔ readr   2.1.3      ✔ forcats 0.5.2 
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag()    masks stats::lag()

data <- read_csv('data/body.csv')

## Rows: 507 Columns: 25
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## dbl (25): Biacromial, Biiliac, Bitrochanteric, ChestDepth, ChestDia, ElbowDi...
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

Run simple regression model

plot(data$Biiliac,data$Height)

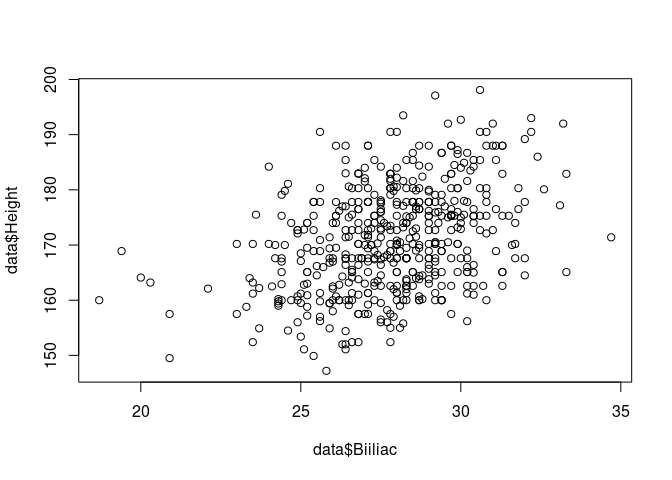The line result <- lm(Height ~ Biiliac, data = data) fits a linear model where Height is the dependent variable and Biiliac is the predictor variable. The line summary(result) provides the results of the model.

# Note: this syntax makes the predict function work
result <- lm(Height ~ Biiliac, data = data)
# Note: This does not work with the predict function: result <- lm(data$Height ~ data$Biiliac)
summary(result)

## 
## Call:
## lm(formula = Height ~ Biiliac, data = data)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -20.6424  -6.6158  -0.1255   6.1055  23.7281 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 125.8837     4.8964  25.709   <2e-16 ***
## Biiliac       1.6263     0.1754   9.272   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 8.705 on 505 degrees of freedom
## Multiple R-squared:  0.1455, Adjusted R-squared:  0.1438 
## F-statistic: 85.98 on 1 and 505 DF,  p-value: < 2.2e-16

If we wish to know how the F-value was calculated we can ask for the anova table.

anova(result)

## Analysis of Variance Table
## 
## Response: Height
##            Df Sum Sq Mean Sq F value    Pr(>F)    
## Biiliac     1   6515  6514.6  85.978 < 2.2e-16 ***
## Residuals 505  38264    75.8                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Compare with correlation

Here we use the cor.test function to calculate the correlation between the two variables. The line correlation$estimate^2 squares the correlation coefficient to get the R-squared value. This is the same as the R-squared value from the linear model.

correlation <- cor.test(data$Height, data$Biiliac)
correlation

## 
##  Pearson's product-moment correlation
## 
## data:  data$Height and data$Biiliac
## t = 9.2724, df = 505, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.3044541 0.4534453
## sample estimates:
##       cor 
## 0.3814241

correlation$estimate^2

##       cor 
## 0.1454843

Get the predicted values

Below, we generate the predicted values for the existing data and for new data. The line fitted <- fitted.values(result) generates the predicted values for the existing data. The line predicted <- predict(result, newdata=new_data) generates the predicted values for new data.

For the existing independent variable values

fitted <- fitted.values(result)
plot(data$Biiliac,data$Height)
points(data$Biiliac, fitted, col='red')

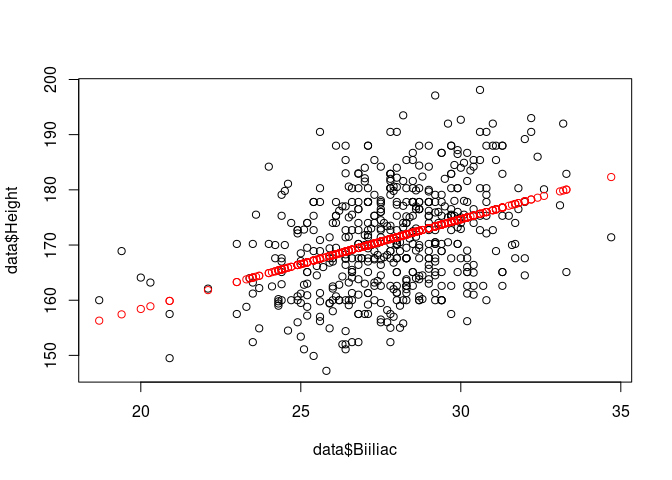
For new independent variable values

More general prediction:

new_independent_values <- c(10,15, 20, 25, 30, 35, 40)
new_data <- data.frame(Biiliac = new_independent_values)

predicted <- predict(result, newdata=new_data)

plot(data$Biiliac, data$Height, col='black')
points(new_independent_values,predicted, col='blue', cex=2, pch=16)
points(data$Biiliac, fitted, col='red')

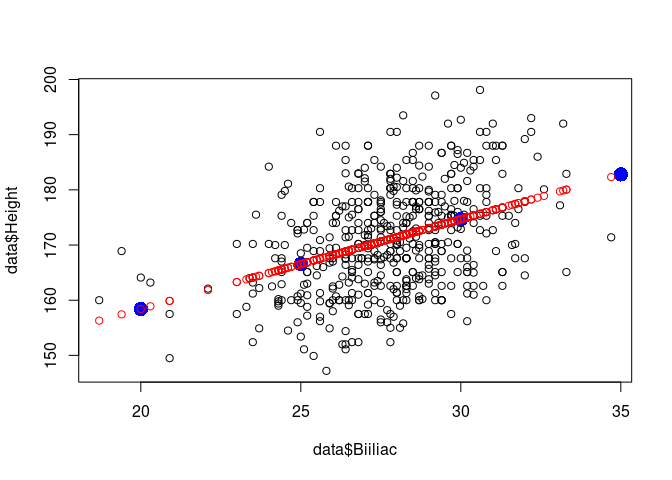
Second example: Vik data

vik_data <- read_csv('data/vik_table_9_2.csv')

## Rows: 12 Columns: 4
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## dbl (4): Person, Y, X1, X2
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

plot(vik_data$X1, vik_data$Y)

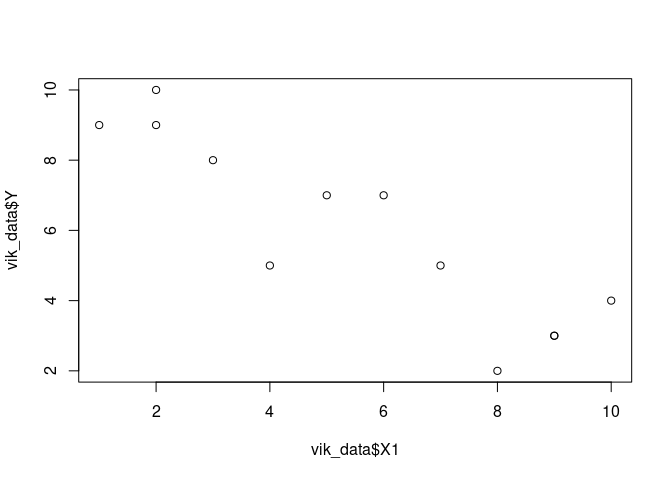
result <- lm(Y ~ X1, data=vik_data)
summary(result)

## 
## Call:
## lm(formula = Y ~ X1, data = vik_data)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -2.1635 -0.3365  0.1121  0.7804  1.4907 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  10.2664     0.7561  13.579 9.07e-08 ***
## X1           -0.7757     0.1208  -6.421 7.63e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.25 on 10 degrees of freedom
## Multiple R-squared:  0.8048, Adjusted R-squared:  0.7853 
## F-statistic: 41.23 on 1 and 10 DF,  p-value: 7.627e-05

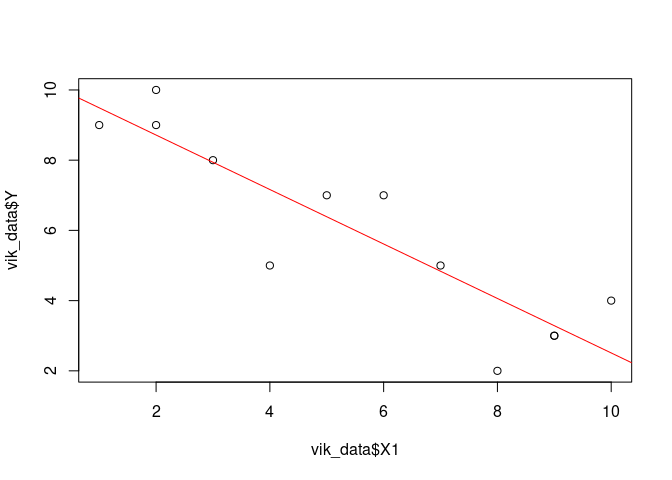
Easier regression line

plot(vik_data$X1, vik_data$Y)
abline(result, col='red')

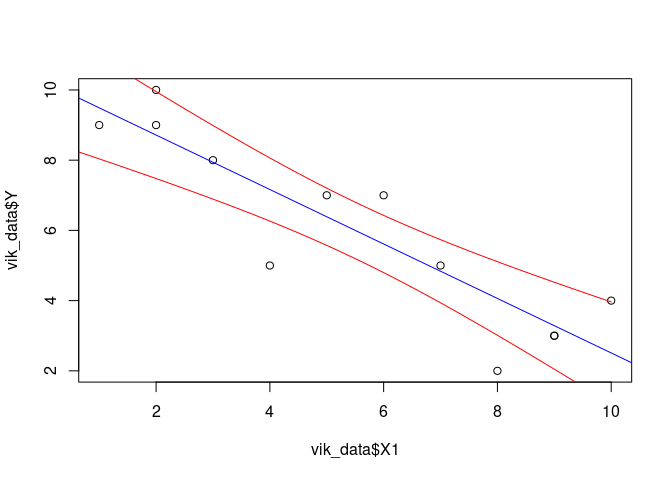
Confidence intervals

Confidence intervals for the predictions

So far, we only generated the best predictions given the model (these are point estimates). However, we can also take into account the uncertainty of the model and generate confidence intervals. Chapter 4 of Faraway, 2009, Linear models with R, provides theory and R code. Here is an example.

The line predicted <- predict(result, newdata=new_data, interval='confidence') generates the 95% confidence intervals. The line lines(new_data$X1, predicted[,2], col='red') plots the lower bound of the confidence interval, and the line lines(new_data$X1, predicted[,3], col='red') plots the upper bound of the confidence interval.

new_data <- data.frame(X1 = seq(0, 10, 0.1))
predicted <- predict(result, newdata=new_data, interval='confidence')
plot(vik_data$X1, vik_data$Y)
lines(new_data$X1, predicted[,2], col='red')
lines(new_data$X1, predicted[,3], col='red')
abline(result, col='blue')

Confidence intervals for the coefficients

We can get the confidence intervals for the estimated coefficients.

confint(result)

##                 2.5 %     97.5 %
## (Intercept)  8.581723 11.9509870
## X1          -1.044883 -0.5065185