Simple Example of Linear Model
Last Updated: 14, November, 2024 at 09:02
This file shows the code used for the output on the slides.
A first example
Before starting download the following data sets:
vik_table_9_2.csvbody.csv
Read and create data data
data<-read.csv('data/vik_table_9_2.csv')
# Let's create two variables that could represent the age and weight of penguins
data$age<- 15 - data$X1
data$weight<-data$Y + 45
plot(data$age, data$weight)
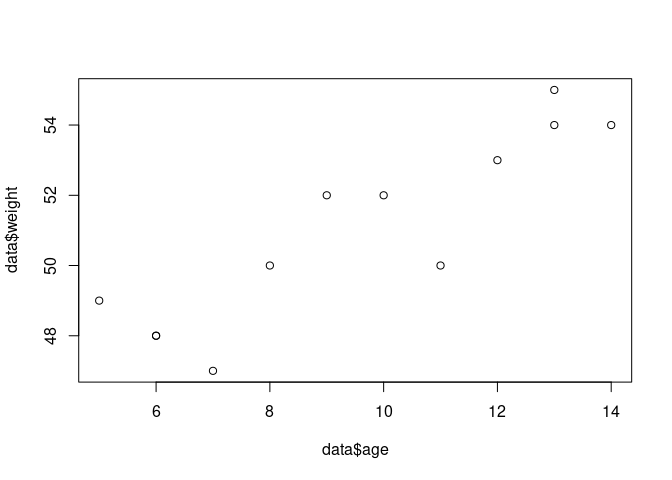
Run a simple linear model
Here, we fit a simple linear model to the data. The line
model1<-lm(weight ~ age, data=data) fits a linear model where weight
is the dependent variable and age is the predictor variable. The line
summary(model1) provides the results of the model.
model1<-lm(weight ~ age, data=data) # fit this model: weight = B0 + B1 * age + error
summary(model1)
##
## Call:
## lm(formula = weight ~ age, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.1635 -0.3365 0.1121 0.7804 1.4907
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 43.6308 1.2031 36.267 6.04e-12 ***
## age 0.7757 0.1208 6.421 7.63e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.25 on 10 degrees of freedom
## Multiple R-squared: 0.8048, Adjusted R-squared: 0.7853
## F-statistic: 41.23 on 1 and 10 DF, p-value: 7.627e-05
Get the F value components
If we wish to know how the F-value was calculated we can ask for the anova table.
anova(model1)
## Analysis of Variance Table
##
## Response: weight
## Df Sum Sq Mean Sq F value Pr(>F)
## age 1 64.383 64.383 41.227 7.627e-05 ***
## Residuals 10 15.617 1.562
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Explicit model comparison
All model assessment is based on comparing models. Here we explicitly compare compare the simplest model (zero predictors, $y_i = \bar{y}$) with a more complex model (a model with one predictor). Per default, R will compare any model you fit to the simplest model using an F-test. However, here we explicitly fit the simplest model and then compare it to the more complex model.
Simple model
First, run the simple model…
data$average_weight <- mean(data$weight) # Create a new variable which is the average of all weights
simple_model <- lm(weight ~ average_weight, data = data)
summary(simple_model)
##
## Call:
## lm(formula = weight ~ average_weight, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.00 -2.25 0.00 2.25 4.00
##
## Coefficients: (1 not defined because of singularities)
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 51.0000 0.7785 65.51 1.3e-15 ***
## average_weight NA NA NA NA
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.697 on 11 degrees of freedom
More complex model
Let’s run the more complex model (again)…
complex_model<-lm(weight ~ age, data=data)
Compare the models
Compare the following output with that of the of the complex model.
anova(simple_model, complex_model)
## Analysis of Variance Table
##
## Model 1: weight ~ average_weight
## Model 2: weight ~ age
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 11 80.000
## 2 10 15.617 1 64.383 41.227 7.627e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
anova(complex_model)
## Analysis of Variance Table
##
## Response: weight
## Df Sum Sq Mean Sq F value Pr(>F)
## age 1 64.383 64.383 41.227 7.627e-05 ***
## Residuals 10 15.617 1.562
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Second example
data <- read.csv('data/body.csv')
data<-data[1:20,]
head(data)
## Biacromial Biiliac Bitrochanteric ChestDepth ChestDia ElbowDia WristDia
## 1 42.9 26.0 31.5 17.7 28.0 13.1 10.4
## 2 43.7 28.5 33.5 16.9 30.8 14.0 11.8
## 3 40.1 28.2 33.3 20.9 31.7 13.9 10.9
## 4 44.3 29.9 34.0 18.4 28.2 13.9 11.2
## 5 42.5 29.9 34.0 21.5 29.4 15.2 11.6
## 6 43.3 27.0 31.5 19.6 31.3 14.0 11.5
## KneeDia AnkleDia Shoulder Chest Waist Navel Hip Thigh Bicep Forearm Knee
## 1 18.8 14.1 106.2 89.5 71.5 74.5 93.5 51.5 32.5 26.0 34.5
## 2 20.6 15.1 110.5 97.0 79.0 86.5 94.8 51.5 34.4 28.0 36.5
## 3 19.7 14.1 115.1 97.5 83.2 82.9 95.0 57.3 33.4 28.8 37.0
## 4 20.9 15.0 104.5 97.0 77.8 78.8 94.0 53.0 31.0 26.2 37.0
## 5 20.7 14.9 107.5 97.5 80.0 82.5 98.5 55.4 32.0 28.4 37.7
## 6 18.8 13.9 119.8 99.9 82.5 80.1 95.3 57.5 33.0 28.0 36.6
## Calf Ankle Wrist Age Weight Height Gender
## 1 36.5 23.5 16.5 21 65.6 174.0 1
## 2 37.5 24.5 17.0 23 71.8 175.3 1
## 3 37.3 21.9 16.9 28 80.7 193.5 1
## 4 34.8 23.0 16.6 23 72.6 186.5 1
## 5 38.6 24.4 18.0 22 78.8 187.2 1
## 6 36.1 23.5 16.9 21 74.8 181.5 1
Relationship between two variables: correlation
correlation_test<-cor.test(data$Wrist, data$Age)
correlation_test
##
## Pearson's product-moment correlation
##
## data: data$Wrist and data$Age
## t = 1.0465, df = 18, p-value = 0.3092
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.2271038 0.6166544
## sample estimates:
## cor
## 0.2394848
correlation_test$estimate**2
## cor
## 0.05735295
Relationship between two variables: linear model
Notice how the t-test for the parameter for x gives the same results
as the t-test for the correlation test.
model2<-lm(data$Wrist~data$Age)
summary(model2)
##
## Call:
## lm(formula = data$Wrist ~ data$Age)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.1170 -0.7277 -0.2141 0.7566 1.5516
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 15.73914 1.56466 10.059 8.16e-09 ***
## data$Age 0.06860 0.06555 1.047 0.309
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.8297 on 18 degrees of freedom
## Multiple R-squared: 0.05735, Adjusted R-squared: 0.004984
## F-statistic: 1.095 on 1 and 18 DF, p-value: 0.3092