Logic of F

Last Updated: 14, November, 2024 at 08:42

Data

Data

Here, I provide some data and fit the model. I also plot the prediction of the base model and the augmented model.

independent <- c(54,46,42,50,43,41,46,39,37,45,45,41,54)
dependent <-c(601,579,572,617,566,547,597,580,536,579,576,601,664)

mean_independent <- mean(dependent)

model <-lm(dependent~independent)

plot(independent, dependent)
abline(model, col='red', lwd=3, lty=3)
abline(h=mean_independent, col='blue', lwd=3, lty=3)

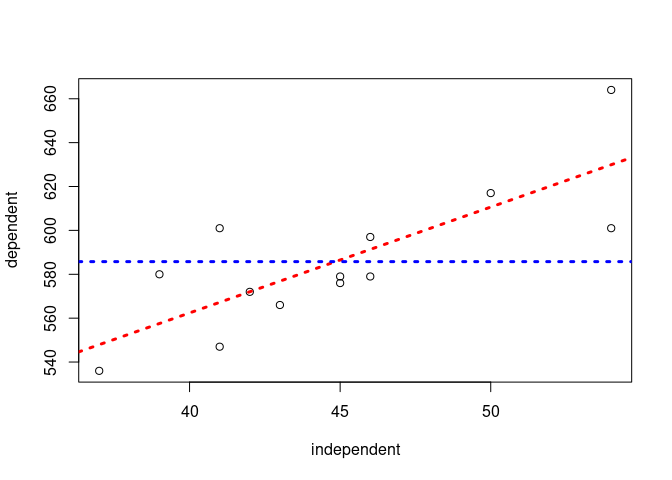
Here, I calculate the three sum of squares. These can be compared with the anova table.

predictions <- predict(model)
mean_predictions <-mean(predictions)

summary(model)

## 
## Call:
## lm(formula = dependent ~ independent)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -28.922 -11.924  -7.511   6.372  34.078 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  369.457     51.084   7.232 1.68e-05 ***
## independent    4.823      1.132   4.261  0.00134 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 20.68 on 11 degrees of freedom
## Multiple R-squared:  0.6228, Adjusted R-squared:  0.5885 
## F-statistic: 18.16 on 1 and 11 DF,  p-value: 0.00134

anova(model)

## Analysis of Variance Table
## 
## Response: dependent
##             Df Sum Sq Mean Sq F value  Pr(>F)   
## independent  1 7763.5  7763.5  18.159 0.00134 **
## Residuals   11 4702.8   427.5                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

ss_residuals <- sum(model$residuals^2)
ss_predictions <- sum((predictions - mean_predictions)^2)
ss_total <- sum((dependent - mean_independent)^2)

txt1 <- sprintf('ss total: %.2f', ss_total)
txt2 <- sprintf('ss predictions: %.2f', ss_predictions)
txt3 <- sprintf('ss residuals: %.2f', ss_residuals)

print(txt1)

## [1] "ss total: 12466.31"

print(txt2)

## [1] "ss predictions: 7763.48"

print(txt3)

## [1] "ss residuals: 4702.83"

Now, I am ready to calculate the F and its nominator and denominator. These can be compared with the anova table.

nominator <- (ss_total-ss_residuals)/1
denominator <- ss_residuals/model$df.residual

f = nominator / denominator
print(nominator)

## [1] 7763.482

print(denominator)

## [1] 427.5297

print(f)

## [1] 18.15893