Basic Programming

Last Updated: 26, October, 2025 at 17:53

Basics of programming: variables and functions

Programming is basically (1) storing data, (2) performing operations on this data.

We will store data in so-called variables. We use functions to perform operations on the data. We will also learn about flow control which allows us to execute code depending on conditions or to repeat code. Finally, objects combine data and functions.

Basic operations: R as a calculator

R can perform the classic operations.

1 / 200 * 30

## [1] 0.15

(59 + 73 + 2) / 3

## [1] 44.66667

sin(pi / 2)

## [1] 1

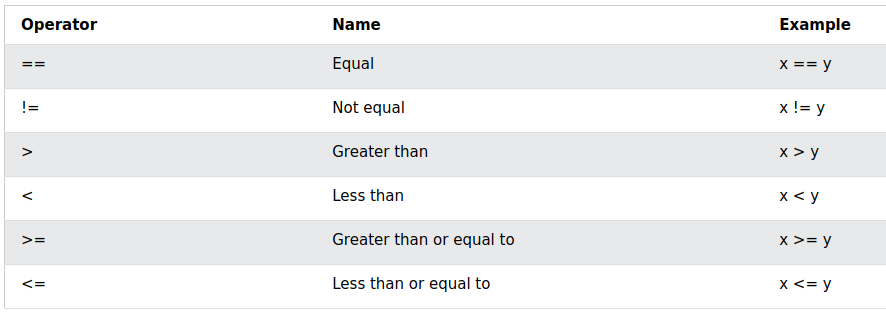
Logical operations

5 > 6

## [1] FALSE

5 + 1 == 6 #NOTE: I am using == to check equality!

## [1] TRUE

1234 != 1234

## [1] FALSE

Storing data in variables

Assigning data to a variable

R uses <- to make assignments. This is a pain to type. You could use = but it will cause confusion later on.

my_variable <- 5

Both <- and = and work in most cases.

x <- 3
x = 3

…but R programmers use <- for assignments.

score <- 100

mean(x = 1:10)

## [1] 5.5

Why it matters

<- always works.
= sometimes doesn’t (e.g., in loops or formulas).

Types of variables

Variables (also called values) come in many types (or classes). The very basic ones are the following:

my_logical <- TRUE
my_character <- 'this is just a piece of text'
my_numeric <- 1.23455

These are very simple data types. We will often used much more complex ones when working with actual data.

Name <- c("Jon", "Bill", "Maria", "Ben", "Tina")
Age <- c(23, 41, 32, 58, 26)
my_data_frame <- data.frame(Name, Age)

R studio shows values and data separately in the Environment window. However, this is just a visualization used by R studio. You can use this window to inspect variables!

Note on naming variables

Try to use descriptive names for variables. And try to stick to a naming convention that works for you - preferably one that makes your code easy to read.

i_like_snake_case <- 'snake_case'
otherPeopleUseCamelCase <- 'CamelCase'
some.people.use.periods <- 'periods.are.allowed'
And_aFew.People_DONTLIKEconventions <- 'Madness, Madness, I tell you!'

From R for Data Science:

There’s an implied contract between you and R: it will do the tedious computation for you, but in return, you must be completely precise in your instructions. Typos matter. Case matters.

Also, it is important that you use names that are not keywords or functions in R. For example, the following is a bad idea:

#length <- 15 ## THIS IS A BAD IDEA

Trick 1: Using the up and down keys

You can use the up and down keys to navigate through the history of commands you’ve entered. This is a very useful feature.

The vector

The vector is another basic variable in R. It’s the simplest type of variable that actually allows you to store something recognizable as ‘data’. We will spend some time on vectors as they are a good place to start to work with relatively simple data. Also, understanding how to work with vectors makes working with more complex data easier. Much of the operations you can do on vectors, which are 1D, can also be done on 2D data frames.

Creating a vector manually

a_vector <- c(1, 5, 4, 9, 0) # Technically an atomic vector
another_one <- c(1, 5.4, TRUE, "hello") # Technically, this is a list

Creating a vector using the : operator

x <- 1:7
y <- 2:-2

Using seq to make a vector

step_size <- seq(1, 10, by=0.25)
length_specified <- seq(1, 10, length.out = 20)

Indexing vectors

Every item in a vector has an index. Vector indices in R start from 1, unlike most programming languages where index start from 0.

my_longer_vector <- c(1, 2, 'three', '4', 'V', 6, 7, 8)

You can use the [] to select (multiple) elements from a vector.

my_single_element <- my_longer_vector[5]
the_start <- my_longer_vector[1:3]
my_part_of_vector <- my_longer_vector[c(1, 2, 5)] # I'm using a vector to select parts of a vector. Life is funny.

You can also use [] to overwrite a part of a vector

my_longer_vector[1:3] <- c('replace', 'this', 'now')

Logical vectors

vector1 <- c(1,5,6,7,2,3,5,4,6,8,1,9,0,1)
binary_vector <- vector1 > 5
binary_vector

##  [1] FALSE FALSE  TRUE  TRUE FALSE FALSE FALSE FALSE  TRUE  TRUE FALSE  TRUE
## [13] FALSE FALSE

some_other_vector <- seq(from = 0, to = 100, length.out = length(vector1))
selected <- some_other_vector[binary_vector]
selected

## [1] 15.38462 23.07692 61.53846 69.23077 84.61538

Another trick

Before we go on, I want to share a simple trick. Using an IDE like Rstudio makes life easier (or at least it should). One of the benefits of the IDE is tab-completion.

[DEMO GOES HERE]

Functions

Now we know how to store data, we can start manipulating the data using functions.

Functions take 0 or more inputs (also called arguments), perform some operation (i.e., the function of the function), and return some output. This output can be complex and consist of multiple parts. These are generic ways in which functions are used:

output <- function_name(arg1 = val1, arg2 = val2, ...)
output <- function_name(val1, val2, ...)

We’ve already encountered a function:

output<-seq(from = 1, to= 123, by = 0.123)

How do we know which arguments a function can take? Using the help:

?seq

Some very simple functions that might be useful.

a <- max(output)
b <- mean(output)
c <- min(output)
d <- ceiling(output)
e <- sd(output)

Here is a function which returns more complex data. At this point, you’re not supposed to know what this function does (it fits a regression line). The point is that it returns complex data with multiple fields.

x <- runif(100)
y <- 10 + 5 * x + rnorm(100)
result <- lm(y ~ x)
print(result)

## 
## Call:
## lm(formula = y ~ x)
## 
## Coefficients:
## (Intercept)            x  
##      10.059        5.094

Getting Help

Built-in Help

R has built-in help. Learning how to use it will save you some frustration.

You can use ?function_name to get help on a specific function. For example, here we get some help on the lm() function, a function to fit linear models. We will be using this function a lot.

?lm

or

help(lm)

You can also get an example of how to use a function using example(function_name).

example(lm)

## 
## lm> require(graphics)
## 
## lm> ## Annette Dobson (1990) "An Introduction to Generalized Linear Models".
## lm> ## Page 9: Plant Weight Data.
## lm> ctl <- c(4.17,5.58,5.18,6.11,4.50,4.61,5.17,4.53,5.33,5.14)
## 
## lm> trt <- c(4.81,4.17,4.41,3.59,5.87,3.83,6.03,4.89,4.32,4.69)
## 
## lm> group <- gl(2, 10, 20, labels = c("Ctl","Trt"))
## 
## lm> weight <- c(ctl, trt)
## 
## lm> lm.D9 <- lm(weight ~ group)
## 
## lm> lm.D90 <- lm(weight ~ group - 1) # omitting intercept
## 
## lm> ## No test: 
## lm> ##D anova(lm.D9)
## lm> ##D summary(lm.D90)
## lm> ## End(No test)
## lm> opar <- par(mfrow = c(2,2), oma = c(0, 0, 1.1, 0))
## 
## lm> plot(lm.D9, las = 1)      # Residuals, Fitted, ...


## 
## lm> par(opar)
## 
## lm> ## Don't show: 
## lm> ## model frame :
## lm> stopifnot(identical(lm(weight ~ group, method = "model.frame"),
## lm+                     model.frame(lm.D9)))
## 
## lm> ## End(Don't show)
## lm> ### less simple examples in "See Also" above
## lm> 
## lm> 
## lm>

You can also search help pages:

??"linear model"
help.search("regression")

The Internet

The R help system is powerful, but most R users also rely on the Internet for quick answers. It’s important to search with context**

r how to merge data frames dply 
r plot regression line ggplot2 
r error object not found`.

Add the word “r” or the package name to every query — otherwise you may get unrelated results. Unfortunately, R is a non-descript name for a programming language.

AI tools

I encourage you to use AI tools but remember you are in charge and responsible for the correctness of your own code.

Give AI tools enough context to work with. For example, instead of just giving the error to an AI tool, copy your code and ask what causes the error.

myata <- data.frame(age = 1:5, score = c(2, 3, 5, 7, 11))
lm(score ~ age, data = mydata)

## Error in eval(mf, parent.frame()): object 'mydata' not found

Tip from the field What I sometimes do is to have AI check my full script (even when I think it works). This sometimes flags up suspicious code that I might want to double-check. It’s an extra pair of eyes to check the code. Below is a very simple example of something that could go wrong. The R parser will see no problems. But AI might flag it up as suspicious.

y <- c(2,3,5,7,11)
X1 <- c(1,2,3,4,5)
X2 <- c(2,6,4,9,15)
X3 <- c(5,3,6,2,1)
model <- lm(y~X1 + X2)
summary(model)

## 
## Call:
## lm(formula = y ~ X1 + X2)
## 
## Residuals:
##       1       2       3       4       5 
##  0.6524 -0.8182  0.1872 -0.5294  0.5080 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)  -0.6310     1.0090  -0.625    0.596
## X1            1.4866     0.6772   2.195    0.159
## X2            0.2460     0.2112   1.165    0.364
## 
## Residual standard error: 0.9134 on 2 degrees of freedom
## Multiple R-squared:  0.9674, Adjusted R-squared:  0.9348 
## F-statistic: 29.69 on 2 and 2 DF,  p-value: 0.03259

> **AI:**  
> The model fits fine, but I notice you created `X3` and didn’t include it in the formula.  
> If that’s intentional, great — but if you meant to test its effect, update the model to:
> ```r
> model <- lm(y ~ X1 + X2 + X3)
> ```
> Small oversights like unused variables are easy to miss, and an automated code review can help catch them.

Flow control in R

You could write all R scripts as a serial statements of functions. However, to fully exploit the power of programming, you would need to learn about flow control. Flow control refers to (1) executing bits of code depending on a condition, and (2) iteratively executing pieces of code.

This is another introduction to flow control.

This is a short script which does one thing after another.

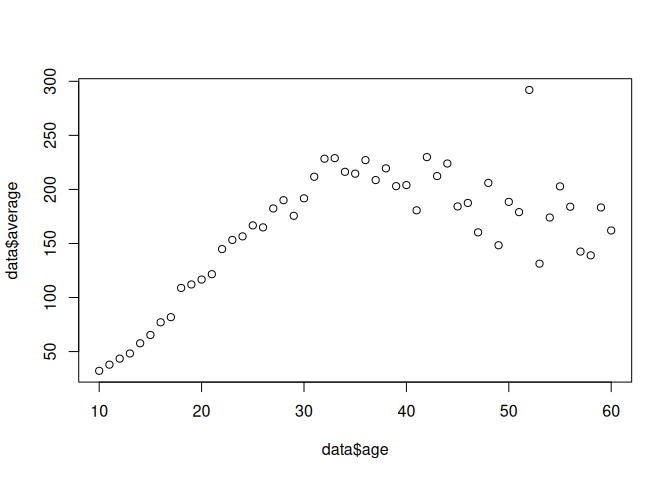
data <- read.csv('data/wages1833.csv')
data$average <- ((data$mnum * data$mwage) + (data$fnum * data$fwage)) / (data$mnum + data$fnum)
model <- lm(data$average ~ data$age)
result <- summary(model)
plot(data$age, data$average )

Overview

Uses of the different flow commands
Keyword Use Example 1 Example 2
if (or, else if) Execute some steps if a condition is true (or false) If the value of a variable is larger than 5, print it to the screen. If the result of a statistical test is significant, add a symbol to the graph.
For Repeat some steps for each item in collection, such as a vector. For each value in a vector, print the value to the screen. Repeat something exactly n times.
While Repeat some steps as long as something is true (or false). As long as the value of a variable is smaller than 5, generate a new value for it.

While your data has outliers, remove them.

The if statement

This is the basic anatomy of an if statement

if (expression) {
   #statement to execute if condition is true
}

Example:

my_number <-12

if (my_number < 20){
  x <- sprintf('%i is less than 20', my_number)
  print(x)
}

## [1] "12 is less than 20"

The if else statement

There is also an if-else variant of this,

a  <- -5
 
# condition
if(a > 0)
{
    print("Positive Number")
}else{
    print("negative number")
}

## [1] "negative number"

Rewriting the previous one on 1 line (maybe that makes it easier to read?)

a  <- -5
 
# condition
if(a > 0){print("Positive Number")}else{print("negative number")}

## [1] "negative number"

The else if statement

a <- 200
b <- 33

if (b > a) {
  print("b is greater than a")
} else if (a == b) {
  print("a and b are equal")
} else {
  print("a is greater than b")
} 

## [1] "a is greater than b"

Overview of if statements

The for loop

The for loop iterates over a sequence.

my_vector <- runif(5)
for (x in my_vector) {
  y <- x * 3
  print(y)
}

## [1] 2.878933
## [1] 2.901794
## [1] 0.3190982
## [1] 2.585775
## [1] 2.924298

Just to drive the point home, another example:

fruits <- list("apple", "banana", "cherry")
for (x in fruits) {
  print(x)
} 

## [1] "apple"
## [1] "banana"
## [1] "cherry"

One very common use of the for loop is to iterate a bit of code exactly n times.

number_of_time_i_want_to_repeat_this <-10
for (x in 1:10) {
  print('This is being repeated!')
} 

## [1] "This is being repeated!"
## [1] "This is being repeated!"
## [1] "This is being repeated!"
## [1] "This is being repeated!"
## [1] "This is being repeated!"
## [1] "This is being repeated!"
## [1] "This is being repeated!"
## [1] "This is being repeated!"
## [1] "This is being repeated!"
## [1] "This is being repeated!"

You can use a break statement to break the loop at any point.

number_of_time_i_want_to_repeat_this <-10
for (x in 1:10) {
  print('This is being repeated!')
  if (x > 7){
    print('I quit!')
    break
  }
} 

## [1] "This is being repeated!"
## [1] "This is being repeated!"
## [1] "This is being repeated!"
## [1] "This is being repeated!"
## [1] "This is being repeated!"
## [1] "This is being repeated!"
## [1] "This is being repeated!"
## [1] "This is being repeated!"
## [1] "I quit!"

The while loop

The while repeats a piece of code if something is true and as long as it is true.

i <- 1
while (i < 6) {
  print(i)
  i <- i + 1
} 

## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5

The break keyword

You can use break to exit a loop at any time

i <- 1
while (i < 100000) {
  print(i)
  i <- i + 1
  if (i > 5){break}
} 

## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5

Exercises: Flow control

Solutions

One

Write a for loop that iterates over the numbers 1 to 7 and prints the cube of each number using print().

for(i in 1:7){
  print(i^2)
  }

## [1] 1
## [1] 4
## [1] 9
## [1] 16
## [1] 25
## [1] 36
## [1] 49

Two

Write a while loop that prints out standard random normal numbers (use rnorm()) but stops (breaks) if you get a number bigger than 1.

Option 1

value <- 0
counter <-0
while(value < 1)
{
  value <- rnorm(1)
  counter <- counter + 1
}
print(value)

## [1] 1.954834

print(counter)

## [1] 5

Option 2

counter <-0
while(TRUE)
{
  value <- rnorm(1)
  counter <- counter + 1
  if (value > 1){break}
}
print(value)

## [1] 1.362865

print(counter)

## [1] 10

Three

Using a for loop simulate the flip a coin twenty times, keeping track of the individual outcomes (1 = heads, 0 = tails) in a vector.

repeats <- 20
outcomes <- character(repeats)
for(i in 1:repeats)
{
  outcome <- sample(c('H','T'), 1)
  outcomes[i] <- outcome
}
outcomes

##  [1] "H" "H" "H" "T" "T" "H" "T" "T" "H" "T" "T" "H" "T" "H" "H" "T" "T" "H" "T"
## [20] "H"

You could do this in one line (but that was not the exercise).

repeats <- 20
outcomes <- sample(c('H','T'), repeats, replace = TRUE)
outcomes

##  [1] "H" "H" "H" "T" "T" "T" "T" "T" "T" "H" "T" "T" "H" "T" "T" "T" "T" "H" "H"
## [20] "T"

Four

Use a while loop to investigate the number of terms required before the series 1 ,reaches above 10 million.

product <- 1
term <- 0

while(product < 10000000)
{
  term <- term + 1
  product <- product * term
  
}
print(term)

## [1] 11

# Check
1:term

##  [1]  1  2  3  4  5  6  7  8  9 10 11

cumprod(1:term)>10000000

##  [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE

Note on vector preallocation

This piece of code builds a vector by appending numbers to the end of it.

repeats <- 10000
startTime <- Sys.time()
my_vector <- c()
for (i in 0:repeats){
  x <- runif(1)
  vector <- append(vector, x)
}
endTime <- Sys.time()
print(sprintf('Duration: %.2f', endTime - startTime))

## [1] "Duration: 0.43"

This piece of code preallocates a vector and is more efficient.

repeats <- 10000
startTime <- Sys.time()
my_vector <- numeric(repeats)
for (i in 0:repeats){
  x <- runif(1)
  vector[i] <- x
  }
endTime <- Sys.time()
print(sprintf('Duration: %.2f', endTime - startTime))

## [1] "Duration: 0.03"

Working with text: the paste() function

x <- runif(100)
y <- 10 + 5 * x + rnorm(100)
result <- lm(y ~ x)
summary(result)

## 
## Call:
## lm(formula = y ~ x)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -2.4195 -0.7328 -0.0227  0.6718  3.4195 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  10.0538     0.1936   51.94   <2e-16 ***
## x             4.9407     0.3546   13.93   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.017 on 98 degrees of freedom
## Multiple R-squared:  0.6645, Adjusted R-squared:  0.6611 
## F-statistic: 194.1 on 1 and 98 DF,  p-value: < 2.2e-16

test1 <- paste(10000)
test2<-paste(result$coefficients[1], result$coefficients[2], sep = ', ')
test3<-paste('The coefficients are: ', result$coefficients[1],  ', ', result$coefficients[2], sep='')
print(test1)

## [1] "10000"

print(test2)

## [1] "10.0538038862781, 4.94070059507232"

print(test3)

## [1] "The coefficients are: 10.0538038862781, 4.94070059507232"

for (x in 1:10) {print(test3)}

## [1] "The coefficients are: 10.0538038862781, 4.94070059507232"
## [1] "The coefficients are: 10.0538038862781, 4.94070059507232"
## [1] "The coefficients are: 10.0538038862781, 4.94070059507232"
## [1] "The coefficients are: 10.0538038862781, 4.94070059507232"
## [1] "The coefficients are: 10.0538038862781, 4.94070059507232"
## [1] "The coefficients are: 10.0538038862781, 4.94070059507232"
## [1] "The coefficients are: 10.0538038862781, 4.94070059507232"
## [1] "The coefficients are: 10.0538038862781, 4.94070059507232"
## [1] "The coefficients are: 10.0538038862781, 4.94070059507232"
## [1] "The coefficients are: 10.0538038862781, 4.94070059507232"

Session info (Tech details)

sessionInfo()

## R version 4.3.3 (2024-02-29)
## Platform: x86_64-pc-linux-gnu (64-bit)
## Running under: Linux Mint 22.2
## 
## Matrix products: default
## BLAS:   /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3 
## LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.26.so;  LAPACK version 3.12.0
## 
## locale:
##  [1] LC_CTYPE=en_US.UTF-8       LC_NUMERIC=C              
##  [3] LC_TIME=en_US.UTF-8        LC_COLLATE=en_US.UTF-8    
##  [5] LC_MONETARY=en_US.UTF-8    LC_MESSAGES=en_US.UTF-8   
##  [7] LC_PAPER=en_US.UTF-8       LC_NAME=C                 
##  [9] LC_ADDRESS=C               LC_TELEPHONE=C            
## [11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C       
## 
## time zone: America/New_York
## tzcode source: system (glibc)
## 
## attached base packages:
## [1] stats     graphics  grDevices utils     datasets  methods   base     
## 
## loaded via a namespace (and not attached):
##  [1] compiler_4.3.3    fastmap_1.2.0     cli_3.6.5         tools_4.3.3      
##  [5] htmltools_0.5.8.1 yaml_2.3.10       rmarkdown_2.30    knitr_1.50       
##  [9] xfun_0.53         digest_0.6.37     rlang_1.1.6       evaluate_1.0.5